(2)要知道一个物体的重量,你能举出多少方法来?
(3)用硬纸板做一个圆盘,像钟面那样分成12个格。在12个数码的位置,写上12个抽象的性质,如1.黄色,2.贵重,3.小巧,4.可动,5.有用,6.沉重,7.移动,8.弹性,9.圆形,10.有价值,11.短小,12.耐久。在圆盘中间装一个能灵活转动的指针。这样,就可以来做游戏了:一个人去转动指针,当指针停下来的时候,指针指着一种性质,转动指针的人就举出具有这种性质的事物,也可以一连转二次,举出同时兼备两种性质的事物来,举出的事物越多越好。
(4)六个苹果,用一根5米长的绳子,每隔1米挂一个,正好。现在吃掉了一个苹果,要求还要用这根绳子,仍然是每1米拴一个苹果,绳子不剩,应该怎样拴?
(5)哥哥用绳子做一个直径3米的圆圈,弟弟一下子就跳出去了。哥哥说:“好,我用这条绳再做一个圈,让你永远也跳不出去。”你知道哥哥做的是怎样一个圈吗?
(6)用14根火柴,摆了两只倒扣着的杯子(如图),只要动五根火柴,就可以让杯子的口倒过来,该怎么动呢?
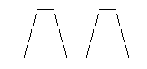
(7)20世纪中有这样一年,把这一年的年份写在纸上,把纸倒过来时纸上的数还是这年年份数,请想出这个年份。
(8)在8与9之间加个什么记号,就可以得到一个大于8和小于9的数。
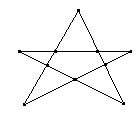
(9)一个人问阿凡提:“阿凡提,你能把10棵小树苗栽成五行,每行都是四棵吗?”阿凡提有点被难住了。你有什么办法吗?
(10)你想一下,你所见到的影子中,什么影子最大?
(11)你吃苹果时,果皮按正常宽度中间不断而连续削下来,平放在桌子上,想象一下是什么形状?
(12)一位猎人带着一只狗上山打猎去了,你能用3笔画出这种情景吗?
(13)有位牧人问阿凡提:“世界上有没有不吃羊的狼?”“有,有。”阿凡提肯定地说。“那是什么狼”,请问。请你想一想。
(14)一个国王想难住一个小神童,问:“王宫前的水共有多少桶。”小神童眨了眨眼睛,说出了令国王满意的答复。你猜一猜,小神童是如何回答的?
(15)世界上什么东西最长又最短、最快又最慢,能分割最小又能扩展到无穷大,最不受人重视而又最受人珍借。没有它,什么事都做不成。那是什么?
(16)这个图形像什么?你说出的越多,证明你想象力越丰富。
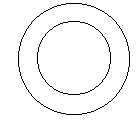
(17)这个图像是什么?
(18)6根火柴放在一起,不折断与弯曲,使其中任何1根火柴都跟其他5根火柴有接触,应如何摆放?
(19)三头牛和三只虎要渡过河去,只有一条小船,每次能运装两头过河,但不能空船回来,为了防止虎吃牛,在一边岸上的牛数不能少于虎数。应该怎样渡?至少需要渡几次?
(20)相传有一天,诸葛亮把将士们召集在一起,说:“你们中间不论谁,从1~1024中任意选出一个整数,记在心里,我提出10个问题,只要求回答‘是’或''不是‘。10个问题全答完以后,我就会’算''出你心里记的那个数。”诸葛亮刚说完,一个谋士站起来说,他已经选好了一个数。诸葛亮问,“你这个数大于512?”谋士答道:“不是。”诸葛亮又向这位谋士提了9个问题。谋士都一一作了回答。诸葛亮最后说:“你记的那个数是1.”谋士听了极为惊奇。因为他选的那个数正好是1.
你知道诸葛亮是怎样运算的吗?
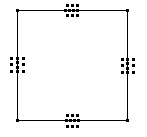
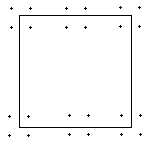
(21)孔明把士兵分成8组,每组人数相等,布成一个正方形的八阵图。以后,他暗暗地把士兵增多,但四方形每边士兵的数目没有增加而总数却增加了。如何增加法,你知道吗?如果原来的排列如图所示,最多能增加多少?
参考答案
(4)把绳子的一头拴在另一头的苹果上,就成了一个圈。
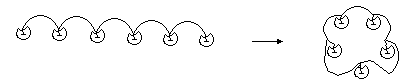
(5)哥哥把绳子绑在弟弟身上,弟弟当然跳不出去了。
(6)照下图移动,杯口可以倒过来
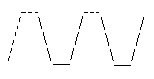
(7)1961年。
(8)加个小数点,得8.9.
(9)如图。
(10)地球的影子,就是夜晚。
(11)如图。
(12)山后面露出猎枪和狗尾巴,如图。
(13)那是死狼或画上的狼。
(14)小神童这样说:“要看多大桶。如桶与水池一样大,那就一桶水;如桶只有水池的一半大,那就是两桶水。
(15)时间。
(18)如图。
(19)需要6次。
①一牛一虎过河,一牛返;②二虎过河,一虎返;③二牛过河,一牛一虎返;④二牛过河,一虎返;⑤二虎过河,一虎返;⑥二虎过河。
(20)1024一半一半地取,取到第10次时,就是“1”。根据这个道理,连续提10个问题,就能找到所需要的数。
(21)最多能增加12个人。
加法如图: